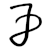Design by Contract

Definitions

Just to make sure that it’s clear what each term is supposed to mean.

The Liskov Substitution Principle

It is defined as:

Every property of objects of type T should hold for all objects of any subtype S of T.

The intent is that code that expects to see something of type T will "just work the same" it it’s actually of a subtype S.
This is overly strict:

Not "every" property!

Types have many properties that are irrelevant for substitutability, such as the implementing code’s time complexity or its maintainability.

Let’s rephrase:

Every code-observable property of objects of type T should hold for all objects of any subtype S of T.

However, even code-observable is too general:

Not even every code-observable property!

Many languages offer a way to enumerate all members of an object, if only for serialisation support.

So: If we take the property “T` has members foo and bar”, if all subclasses must fulfil that property as well, no subclass can have additional members. Clearly, this is not what we want; `T must specify which properties should be relevant to callers and which should not.

We get:

Every property specified for T should hold for all objects of type T and any subtype S of T.

Preconditions and postconditions

Preconditions need to hold before a function is called.
Postconditions need to hold after the function returns.

This can also be worded as a contract:

Each function offers a contract:
IF the caller makes sure that the function’s preconditions are met immediately before the call,
_THEN the function promises that its postconditions hold immediately after it returns.

Not necessarily language-level assertions

Conditions are already useful for documentation, and to decide the more tricky design questions.
If a programming language checks them at runtime, that covers a lot of unit testing.
If a programming language checks them at compile time, they become a validation tool, much like a type system but able to express and validate much more complex conditions.

Few languages and support this, none of them mainstream.
Which is a bit surprising given the simplicity of the idea, though you have to read up on the details to get it right.

What a precondition can use

Preconditions can access the parameters, and any member variables.

Not strictly necessary but good design: If a function is public, use only public members in its precondition - this is called "no hidden clauses in the contract".
This allows callers to check at runtime which preconditions it still needs to fulfil; there are many situations where this is useful.

What a postcondition can use

Postconditions can access parameters, and any member variables.
Postconditions can have hidden clauses without affecting correctness, but they would be distracting if they go into documentation so it is usually better to put that into a normal assert construct inside the function.

In addition, the postcondition must be able to look at the function’s result; in this essay, it will be denoted as result.

For function that do updates, the postcondition may need to access the state as it was before the function was called:

increment_count(int delta)
require no_decrement: delta > 0
ensure count_updated: this.count == old(this.count) + delta

Class invariant

Some explanations of DbC mention class invariants.

These are easy to explain:
They are preconditions on all functions except the constructors.
They also are postconditions on all functions except the destructor, if the language has destructors.

Specification

Preconditions and postconditions can give you amazingly succinct, yet readable specifications.

E.g. here is the square root Javadoc from the JDK:

/**
 * Returns the correctly rounded positive square root of a
 * {@code double} value.
 * Special cases:
 * <ul><li>If the argument is NaN or less than zero, then the result
 * is NaN.
 * <li>If the argument is positive infinity, then the result is positive
 * infinity.
 * <li>If the argument is positive zero or negative zero, then the
 * result is the same as the argument.</ul>
 * Otherwise, the result is the {@code double} value closest to
 * the true mathematical square root of the argument value.
 *
 * @param   a   a value.
 * @return  the positive square root of {@code a}.
 *          If the argument is NaN or less than zero, the result is NaN.
 */
public static double sqrt(double a);

And it does not even specify what "square root" means!

Here’s a rewrite that uses preconditions and postconditions:

/**
 * @ensure
 *   Double.isNan(a) ? Double.isNan(result)
 *   : a < 0.0 ? Double.isNan(result)
 *   : a == Double.POSITIVE_INFINITY ? result == Double.POSITIVE_INFINITY
 *   : a == 0.0 ? result == a
 *   : (result * result - a) <= Math.ulp(result)
 */
public static double sqrt(double a);

Now that’s compact!
Note to the astute reader: The last clause is just an approximation to the real thing.
An accurate postcondition would need functions that check things like "closest to the true mathematical value" and "correctly rounded", which is doable but beyond the scope of this essay.

The list of member functions, revisited

Now we have the tools necessary to answer the question:

[quote]so it
Is the Liskov Substitution Principle applicable if there is a function that enumerates all class members?

Answer: It depends.

Specifically, the class designer decides.
E.g. when the class is serialized to other systems, the API designer will want to decide whether there may be subclasses, and whether these subclasses can have additional fields or not. This is something that receivers of serialized will want to know and deal with, after all.

Design by Contract: Combining LSP and conditions

Subclasses must not tighten preconditions

The caller will be coded against the contract of the superclass.
It will be coded against the preconditions of the superclass, so it won’t assert any preconditions that the subclass may impose in addition.

Exception: You can drop this rule if you already know all subclasses that everybody will ever write, e.g. if you write a library and disallow writing subclasses.
It violates LSP and hence isn’t DbC anymore, it’s a design smell, and the code will be somewhat harder to read and maintain, but it might still be the lesser evil. Just make sure it’s documented for the benefit of the next maintainer!
Usually it’s better to revisit the superclass' contract.

Subclasses must not weaken postconditions.

This is essentially the same as with preconditions, just complementary: The superclass will assume the superclass' postconditions, so you can’t weaken them.

You can tighten them. No harm done, and callers that deal specifically with a subclass may benefit from that.
In some cases, people write subclasses specifically to exploit that.

Subclasses can tighten class invariants

Since an invariant is also a precondition, by the rules above it should never be tightened.
However, it’s it’s the class that establishes it, not the caller.so it

Subclasses still must not weaken invariants. Callers assume the invariant of the superclass.

Practical examples

Each example showcases one of the situations where DbC can help decide.

Squares and rectangles

Consider these classes:

class Rectangle {

  private int x; int y;

  public int getX() { return x; }

  public int getY() { return y; }

  /** ensure getX() == x **/
  public void setX(int x) { this.x = x; }

  /** ensure getY() == y **/
  public void setY(int y) { this.y = y; }
}

That’s easy enough to subclass:

/** @invariant getX() == getY() *//
class Square extends Rectangle {
  private int size;
  public int getX() { return size; }
  public int getY() { return size; }
  public void setX(int x) { this.size = x; }
  public void setY(int y) { this.size = y; }
}

Now, let’s extend Rectangle with a scale operation:

class Rectangle {
  ...
  /** @ensure getX() == old getX() * xFactor && getY() == old getY() * yFactor **/
  public void scale(int xFactor, int yFactor) { this.x == x * xFactor; this.y == y * xFactor; }
}

class Square {
  ...
  public void scale(int xFactor, int yFactor) { /* ??? */ }
}

The question marks are where the problem happens: Square cannot implement both Square's invariant and scale's postcondition, they contradict each other.

What can be done?

Restrict `Square.scale`

Throw an exception in Square.scale if the factors are not the same.
Unfortunately, this essentially adds a precondition to Square.scale: @require xFactor == yFactor, throwing the LSP out of the window.

Avoid updates

Replace the setters with functions that create new objects.
This has obvious performance disadvantages. For runtimes with reference-counting or manual garbage collection, this disadvantage is typically inacceptable; with copying collectors, it merely increases the number of garbage collection runs, but since you ẃant these runs to stay below maybe 5% of overall CPU cycles, it is negligible for most scenarios.

For setters, you’d have with functions such as:

public Rectangle withX(int x) { return new Rectangle(x, this.y); }

withX still returns a Rectangle even in the Square subclass, so it’s the caller’s obligation to deal with the types.
For scale, the caller would have to deal with the situation that the returned object is a Rectangle instead of a Square.

If you want the caller to have a Square, you could add a second scale function:

class Rectangle {
  public Rectangle scale(int factor)
  public Rectangle scale(int xFactor, yFactor)
class Square {
  public Square scale(int factor) // overrides return type
  // No override for scale(int, int), it's already fine

Even setters are problematic

Let’s revisit Rectangle.setX:

/** ensure getX() == x **/
public void setX(int x) { this.x = x; }

Actually, few programmers would expect setX to modify the value returned by getY. Or any other property of Rectangle. Or properties added in subclasses of Rectangle, say, the color in a ColoredRectangle subclass.

So, you can change the postcondition:

/** ensure getX() == x && equalsExcept(old this, this, Rectangle::getX) **/
public void setX(int x) { this.x = x; }

Conceptual incompatibility between updatable object and LSP

It is not possible to have all three of:

Updatable properties
Liskov Substitution Principle
Ability to add subclasses with invariants that restrict an updatable property

TBD
Show that value types (i.e. read-only ones) are an important abstraction.
Conclude that updates and LSP are essentially incompatible; if you want to freely use subtype hierarchies, you need to work with value types.

Parameter and result types

This is more of a thought experiment, but it explains the result type covariance rule that some (many?) OO languages have.

Let’s move the parameter and result types of a simple function into conditions:

ResultType foo(ParameterType p)

becomes

/** @require p instanceof ParameterType; @ensure result instanceof ResultType **/
Object foo(Object p)

You may strengthen the postcondition, so a subclass can use a narrower result type than the original function.
We have seen that above in scale(int).
This is called a covariant override: When going from class to subclass, the result type of any function can also go from class to subclass.

You may weaken the precondition, i.e. allow a superclass in parameters.
This does not seem very useful, but actually the JDK has such functions, such as in Collections:

public static <T> void copy(List<? super T> dest, List<? extends T> src) {

This could have been done as a member function in Collection<T>:

public void copy(List<? super T> dest) {

meaning: You can copy the elements of this Collection into any Collection that requires an element type of T or a superclass.
Which is actually a useful thing to have.

Last updated: 14 Jul 2024 23:44